¿Qué son los números enteros?
Un número entero es un elemento del conjunto numérico que contiene los números naturales, sus inversos aditivos y el cero. Los enteros negativos, como −1 o −3 (se leen «menos uno», «menos tres», etc.), son menores que todos los enteros positivos (1, 2...) y que el cero. Para resaltar la diferencia entre positivos y negativos, a veces también se escribe un signo «más» delante de los positivos: +1, +5, etc. Cuando no se le escribe signo al número se asume que es positivo.
Vamos a tener entonces:
- Números naturales Ν: 1, 2, 3...
- Inversos aditivos de los números naturales: -1, -2, -3...
- El cero: 0
1.1 Representación Sobre la Recta
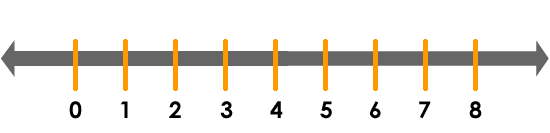
Podemos representar los números naturales en una recta de la siguiente manera:

Potencia es una operación que consiste en multiplicar la base por si mismo tantas veces como indique el exponente
Ejemplo 1:
Ejemplo 2:
El exponente 1 no se escribe (no se pone); por lo tanto todo número que no tiene exponente, se supone que es 1
Todo número (distinto de cero) elevado a 0 es 1.
Realizar el siguientes cuestionario Aqui
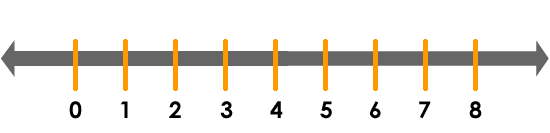
Podemos representar los números naturales en una recta de la siguiente manera:
- trazamos una recta;
- elegimos un punto al que le hacemos corresponder el cero;
- elegimos un segmento cualquiera con un extremo en cero y en el otro extremo marcamos el número uno (1);
- luego transportamos consecutivamente el segmento y marcamos sucesivamente el número 2, el número 3, el número 4, ...
Para
dibujar una recta numérica debemos asegurarnos de que la distancia que
separa dos números sea siempre la misma, es decir, que los números sean
equidistantes entre sí.
Gráficamente,
un número natural es mayor que otro si al representarlo en la recta
está situado más a la derecha (está más lejos del cero).
1.2.Valor Absoluto de un Número Entero
• El valor absoluto de un número entero es la distancia (en unidades) que lo separa del cero en la recta numérica.
• En la práctica se escribe entre dos barras ││
Valor absoluto de −3 se escribe │−3│y es 3.
Valor absoluto de +5 se escribe │+5│y es 5.
Si dos números enteros tienen el mismo valor absoluto pero distinto signo, se llaman opuestos. El opuesto de cero es cero.
Veamos un ejemplo:
│+5│=5 y │−5│= 5 Los números +5 y −5 están a la misma distancia del origen: 5 unidades.
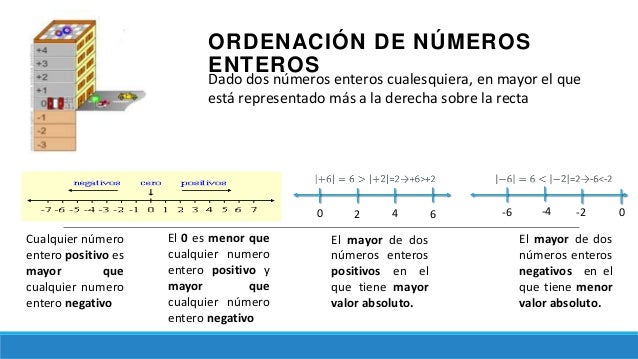
1.3. Ordenación de Números Enteros

Ordenar números enteros a partir de su representación en la recta numérica:
- Entre dos números enteros, es mayor el que más a la derecha está en la recta numérica
- Entre dos números enteros, es menor el que más a la izquierda está en la recta numérica
Ordenar números enteros según su signo y valor absoluto:
- Si dos enteros son positivos, el mayor es el que tiene mayor valor absoluto. Por ejemplo: + 20 > +8
- Cualquier número positivo es mayor que el cero, y el cero es mayor que cualquier negativo. Por ejemplo: +8 >0 > -8
- Entre dos números enteros negativos, es mayor el de menor valor absoluto. Por ejemplo: -8 > –20
2. Operaciones
Con
los números enteros podemos efectuar las mismas operaciones que
realizamos con los numeros naturales: Suma, Resta, Multiplicación
,División, Potencias y Raíces.
2.1. Adición y Sustracción de números enteros
Si los sumandos son del mismo signo, se suman los valores absolutos y al resultado se le pone el signo común.
Ejemplo:
3 + 5 = 8
(−3) + (−5) = −8
Ejemplo:
3 + 5 = 8
(−3) + (−5) = −8
Si los sumandos son de distinto signo, se restan los valores absolutos (al mayor le restamos el menor) y al resultado se le pone el signo del número de mayor valor absoluto.
Sustracción de números enteros
- Para restar dos números enteros se suma al minuendo el opuesto del sustraendo. De esta forma, las rectas se convierten en sumas.
Ejemplo 1:
(+8) - (-6) = (+8) + (+6) = +14
Ejemplo 1:
(-16) - (-8) = (-16) + (+8) = -8
- Cuando se suman enteros positivos y negativos se recomienda agruparlos, esto es, se obtiene la suma de los sumandos positivos y despues la de los negativos; luego se restan los valores absolutos y se escribe al resultado el signo del sumando de mayor valor absoluto.

Potenciación con números enteros
Se utiliza para abreviar la multiplicación de un mismo número cuyo producto se realiza varias veces
El producto a·a·a·a·a·a tiene sus seis factores iguales. Este producto se indica en forma abreviada como a6.
A a6 se llama potencia de base a y exponente 6.
El producto a·a·a·a·a·a tiene sus seis factores iguales. Este producto se indica en forma abreviada como a6.
A a6 se llama potencia de base a y exponente 6.
Potencia es una operación que consiste en multiplicar la base por si mismo tantas veces como indique el exponente
Ejemplo 1:
53 es una potencia que tiene por base 5 y por exponente 3; por eso multiplicamos la base 5 tres veces:
53 = 5·5·5 = 125
Ejemplo 2:
(–3)2 es una potencia de base (–3) y exponente 2; multiplicamos la base (–3) dos veces:
(– 3)2 = (– 3)·(– 3) = 9
Propiedades:
Todo número elevado a 1, es el propio número.
Propiedades:
Todo número elevado a 1, es el propio número.
Ejemplo 3: 51 = 5; 41 = 4: (–11)1 = –11.
El exponente 1 no se escribe (no se pone); por lo tanto todo número que no tiene exponente, se supone que es 1
Todo número (distinto de cero) elevado a 0 es 1.
Ejemplo 4: 110 = 1; 3290 = 1; –70 = –1
Conclusiones:
– Si la base es positiva, el resultado de la operación siempre es positiva sea cual sea el exponente. (en los números naturales la base siempre es positiva)
– Si la base es negativa, el resultado de la operación depende del exponente:
Si el exponente es par el resultado es positivo (el producto de dos signos negativos da resultado positivo: (–)·(–) = +
Si el exponente es impar el resultado es negativo (siempre queda un signo negativo sin aparear).
Para que la base sea negativa tiene que estar entre paréntesis, en cuyo caso también hay que elevar el signo “ – “
Conclusiones:
– Si la base es positiva, el resultado de la operación siempre es positiva sea cual sea el exponente. (en los números naturales la base siempre es positiva)
– Si la base es negativa, el resultado de la operación depende del exponente:
Si el exponente es par el resultado es positivo (el producto de dos signos negativos da resultado positivo: (–)·(–) = +
Si el exponente es impar el resultado es negativo (siempre queda un signo negativo sin aparear).
Para que la base sea negativa tiene que estar entre paréntesis, en cuyo caso también hay que elevar el signo “ – “
Ejemplos:
25 = 2·2·2·2·2 = 32
(– 5)3 = (– 5)·(– 5)·(– 5) = –125 (base negativa con exponente impar: por tanto el signo también se multiplica tres veces).
(–7)4 = (–7)·(–7)·(–7)·(–7) = 2 401 (base negativa con exponente par: el signo se efectúa 4 veces).
– 34 = – 3·3·3·3 = – 81 (la base positiva: se eleva sólo la base y el signo se deja como esta)
(–3)4 = (–3)·(–3)·(–3)·(–3) = 81 (la base negativa y el signo también se eleva).
25 = 2·2·2·2·2 = 32
(– 5)3 = (– 5)·(– 5)·(– 5) = –125 (base negativa con exponente impar: por tanto el signo también se multiplica tres veces).
(–7)4 = (–7)·(–7)·(–7)·(–7) = 2 401 (base negativa con exponente par: el signo se efectúa 4 veces).
– 34 = – 3·3·3·3 = – 81 (la base positiva: se eleva sólo la base y el signo se deja como esta)
(–3)4 = (–3)·(–3)·(–3)·(–3) = 81 (la base negativa y el signo también se eleva).
Realizar el siguientes cuestionario Aqui

